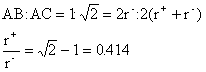無機固体化学演習問題解答
教科書第1章の問題解答は巻末参照のこと。
1.以下の用語を説明し、これらを用いて結晶構造を説明せよ。
格子点、空間格子、単位構造
結晶中の規則正しいイオンなどの配列中、どの点をとってもそれと全く同じ周囲の状況を持つ点を格子点といい、このような点の模様を空間格子という。単位構造は各格子点に存在する原子団であり、結晶構造は空間格子と単位構造を組み合わせることによりあらわすことができる。
2.(1)ブラベー格子を図示せよ。(2)面心正方が存在しない理由を説明せよ。
(2)面心正方格子を空間的に繰り返すとその内部に体心正方格子が存在することを図示できる。この格子は面心正方格子よりも小さな格子で、面心正方格子は体心正方格子であらわせるため存在しない。
3.7つの結晶系を表にまとめよ。
表2・1結晶系の有する対称の要素と格子の種類
| 結晶系 |
軸の長さ および軸角
|
対称軸 |
対称面 |
格子の種類 |
| 2回 |
3回 |
4回 |
6回 |
計 |
| 立方(等軸)晶系 |
a=b=c; α=β=γ=90°
|
6 |
4 |
3 |
0 |
13 |
9 |
P,I,F |
| 正方晶系 |
a=b≠c; α=β=γ=90°
|
4 |
0 |
1 |
0 |
5 |
5 |
P,I |
| 斜方晶系 |
a≠b≠c; α=β=γ=90°
|
3 |
0 |
0 |
0 |
3 |
3 |
P,C,I,F |
| 単斜晶系 |
a≠b≠c; α=γ=90°≠β
|
1 |
0 |
0 |
0 |
1 |
1 |
P,C |
| 三斜晶系 |
a≠b≠c; α≠β≠γ
|
0 |
0 |
0 |
0 |
0 |
0 |
P |
| 六方晶系 |
a=b≠c; α=β=90°,γ=120°
|
6 |
0 |
0 |
1 |
7 |
7 |
P |
| 菱面体晶系 |
a=b=c; α=β=γ≠90°
|
3 |
1 |
0 |
0 |
4 |
3 |
R |
P:単純格子,I:体心格子,F:面心格子(各面の中心にも格子点を有するもの)
C:底面心格子(二つの平行な面の中心にも格子点を有するもの),R:菱面体単純格子
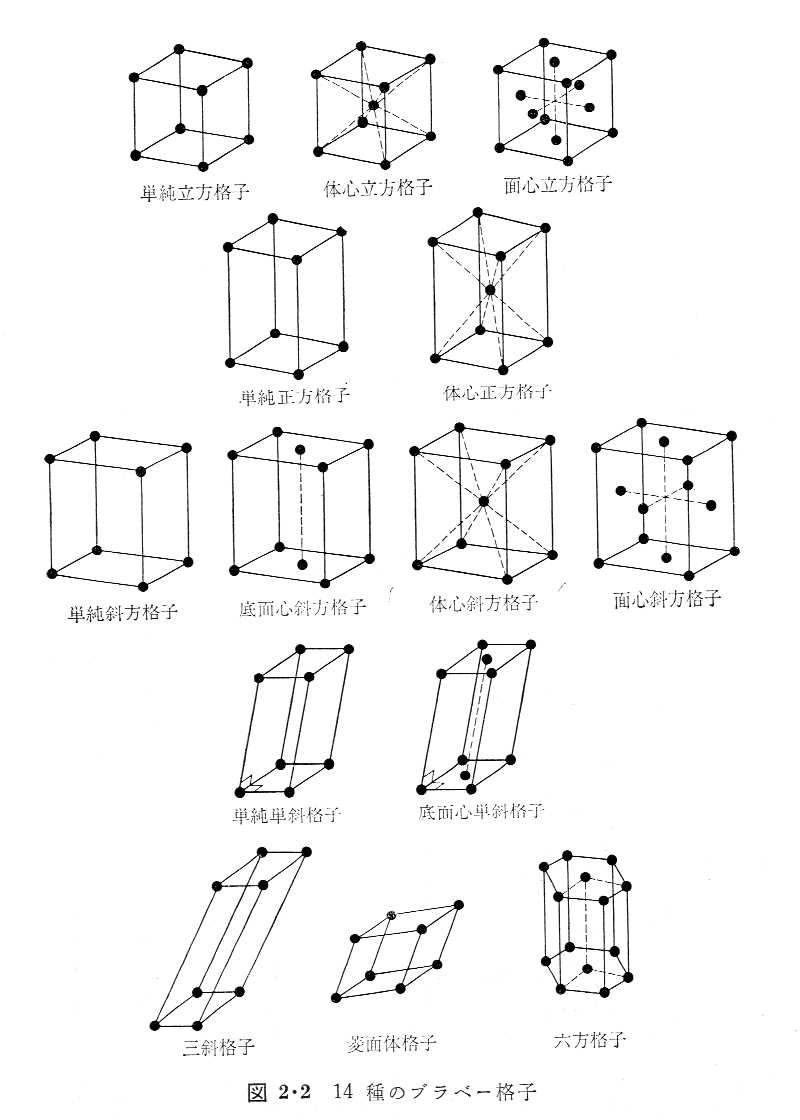
4.立方体の対称操作をすべて図示せよ。
5.ミラー指数(342)および(101)の面を図示せよ。
6.球の最密充填形式を2種類のべよ。
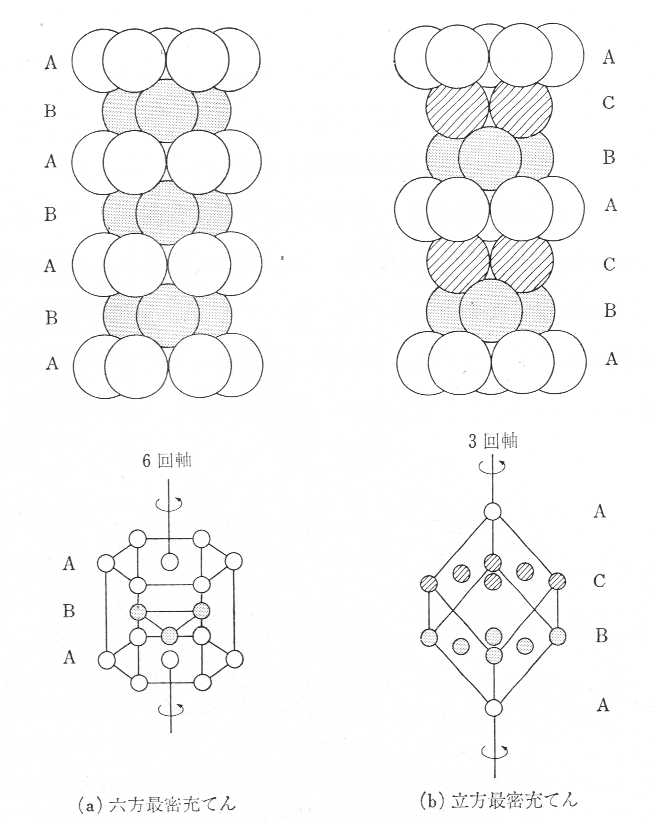
7.一般的に金属元素結晶の構造は球の最密充填形式に基づくが実際の充填形式3種類を述べ、それらの配位数と空間占有率を求めよ。
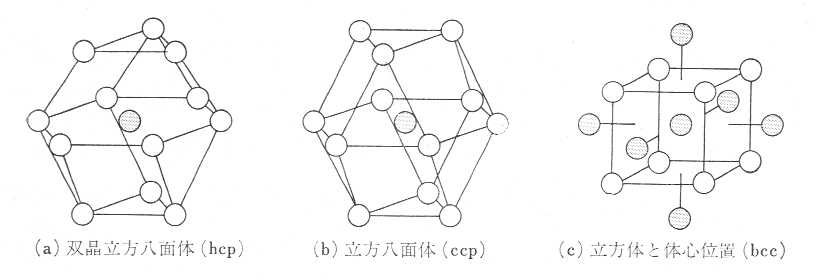
| 充填形式 |
配位数 |
空間占有率/% |
| hcp |
12 |
74 |
| ccp |
12 |
74 |
| bcc |
8 |
68 |
8.球の充填構造には隙間が存在し、その空間に異符号イオンを入れることでイオン結晶の構造を考えることができる。配位数と半径比の関係を表にまとめよ。また、配位数6となる範囲の半径比について計算せよ。
| 配位数 |
安定な配位になれる半径比の範囲 |
配位多面体 |
| 2 |
0〜0.155 |
直線 |
| 3 |
0.155〜0.225 |
三角形 |
| 4 |
0.225〜0.414 |
四面体 |
| 6 |
0.414〜0.732 |
八面体 |
| 8 |
0.732〜1.0 |
立方体 |
| 12 |
1.0 |
立方八面体 |
6配位
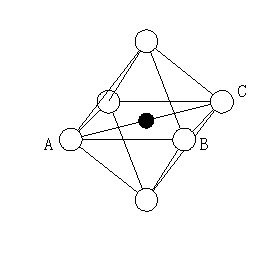
中心陽イオンを含む正方平面を考える。
AB=2r-
正方形の中心に陽イオンがあり、それが頂点の陰イオンと接しているので
AC=2(r++r-)
9.面心立方構造中の八面体位置と四面体位置を図示し、その数を求めよ。
10.2成分化合物の最密充填形式と占有多面体について表にまとめよ。
| 占有多面体の種類と割合 |
最密充てんの形式 |
| |
立方(ccp) |
六方(hcp) |
| 八面体型の全部 |
NaCl |
NiAs |
| 八面体型の半分 |
CdC12 |
CdI2 |
| 四面体型の全部 |
CaF2 |
− |
| 四面体型の半分 |
ZnS |
ZnS |
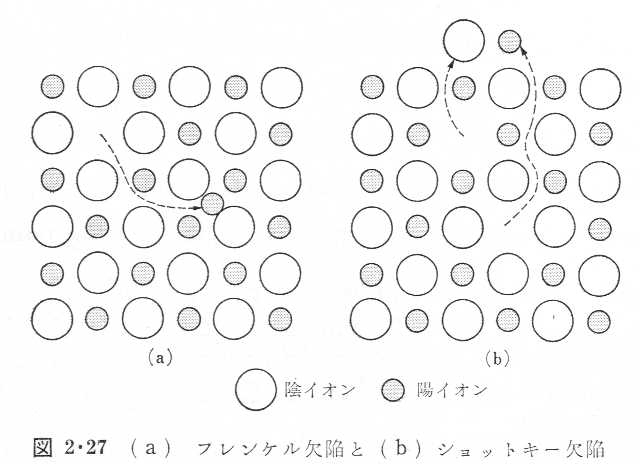
11.フレンケル欠陥とショットキー欠陥を模式的に示せ。
12.図の温度T1において予想される各相の自由エネルギー曲線を図示せよ。
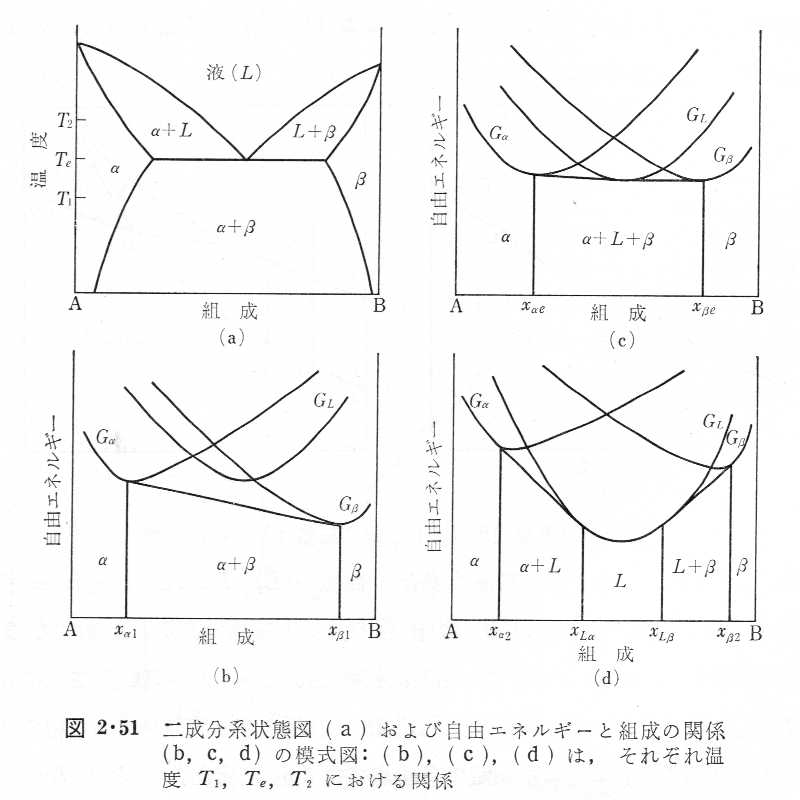
13.
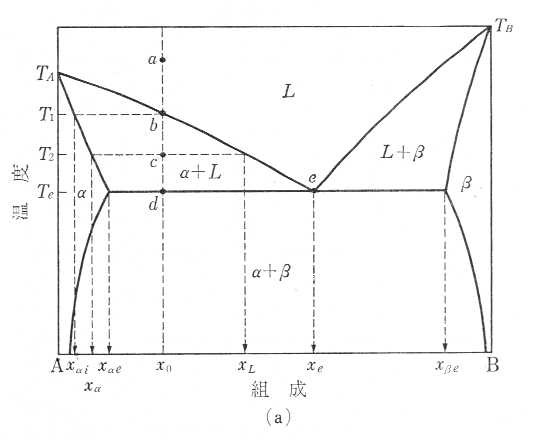
(1)組成x0の液相が点aから点dまで冷却していく過程での反応を説明せよ。
| 点 |
温度 |
相(組成) |
| a |
|
L(x0) |
| b |
T1 |
L(x0)+α(xαi) |
| c |
T2 |
L(xL)+α(xα) |
| d |
T3 |
L(xe)+α(xαe) |
(2)(1)の温度T2において存在する相の組成とその量比を答えよ。
L(xL):α(xα)=|xα-x0|:|xL-x0|
|