無機化学Ⅰ例題集 |
| 例題1・1 核反応方程式を釣り合わせる. 温度の低い赤色巨星の中では中性子捕獲によって重い元素の合成が起こると信じられている.この種の反応の一つは,中性子捕獲によるZnからGaへの変換である.ここでは,まずZnができて,それがβ崩壊する.この全過程の核反応式を書け. 解 中性子捕獲では質量数が1増えるが原子番号は変わらない(したがって,元素としては同じままである).
このとき余分になったエネルギーは光子(γ)として運び去られる.β崩壊では,原子核から電子が1個失われるから,質量数は変わらないが原子番号は1だけ増える.亜鉛は原子番号30だから娘核種はZ=31すなわちガリウムである.したがって核反応式は
(実際には,ニュートリノが1個放出されるが,ニュートリノは質量も電荷もないのでデータからはわからない.) 問題1・1 答え 例題1・2 特性原子遷移のエネルギー. 街灯に使われるナトリウムランフプは波長588nmの特有な黄色光を出す.この光の振動数はいくらか.この光子のモルエネルギーはいくらか(kJmo1-1単位で). 解 振動数は
である.1個の光子のエネルギーは
=3.38×10-19J となる.光子のモルエネルギーEm(単位物質量当たりのエネルギー)は,これにアボ ガドロ定数NA(つまり単位物質量当たりの光子の数)をかけたものに等しい.
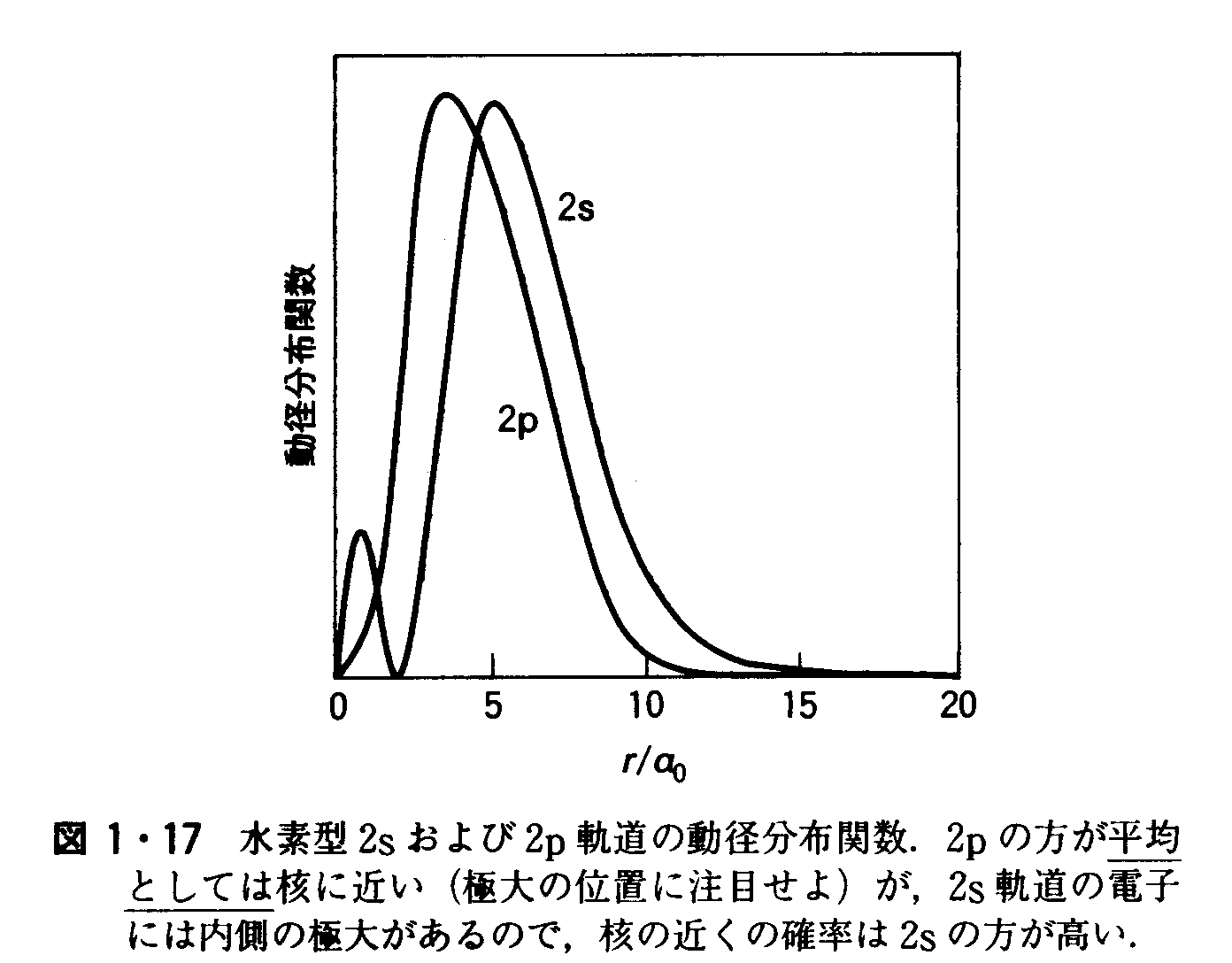
=2.03×105Jmol-1=203kJmol-1 問題1・2 緑色のレーザーをつくるのに用いられるAr+の遷移で放射される514nmの光子のモルエネルギーはいくらか. 答え 3.86×10-19J 例題1・3 動径分布関数の解釈 図1・17は,2sおよび2p波動関数の動径分布関数である.電子が核に近づく確率が高いのはどちらの軌道か.
解 2p軌道の動径分布関数の方が,2s軌道よりも早く核の近くで0に近づく.この違いは,2p軌道が軌道角運動量をもつため核のところで振幅0であることの結果である.したがって,2s電子の方が核に近づく確率は大である. 問題1・3 3pと3dのうち,電子を核の近くに見出す確率の高いのはどちらか. 答え 3p 例題1・4 有効核電荷の効果を説明する.2P電子のZeffは,CよりNの方が大きく,Nより0の方が大きい(表1・4)が,その増加の幅がNとOとの間の方が小さい理由を考えよ.これらの電子配置は C:[He](2s)2(2p)2 N:[He](2s)2(2p)3 0:[He](2s)2(2p)4 である. 解 CからNへ行くとき新たに加わる電子は空の2p軌道に入る.NからOへ行くときには,つぎの電子が入る2p軌道がすでに1個の電子で占められている.したがって,このときに加わった電子はより強い反発を受けるので,核の電荷の増加分が打消される程度はCからNへの場合よりも著しくなる. 問題1・4 BからCへ行くときの2P電子に対する有効核電荷の増加分の方が,LiからBeヘ行くときの2s電子に対する有効核電荷の増加分に比較して大きいことを説明せよ. 答え 加わったp電子がそれぞれ別のp軌道に入るので、遮蔽され方が少ないから。 例題1・5 電子は位置を導く.Ti原子およぴTi3+イオンの基底状態電子配置を示せ.解Z=22だから,原子にするためには,同数の電子を上に示した順序に従って,一つの軌道には2個以内になるように入れていく.こうして得られる電子配置は Ti(1s)2(2s)2(2p)6(3s)2(3p)6(4s)2(3d)2または[Ar](4s)2(3d)2 で,2個の3d電子はスピンを平行にして別々のd軌道に入る.しかしながら,Caを過ぎると3d軌道の方が4s軌道より低くなることを考えると,これらの軌道の順序を逆転させる方が実情をよく反映する.したがって,電子配置は[Ar](3d)2(4s)2と書かれる.イオンの電子配置を得るには,まずs電子を,ついでd電子を必要な数だけ取除けばよい.ここでは,合計3個の電子,つまり,2個のs電子と1個のd電子とを取除けばよい.したがって,Ti3+の電子配置は[Ar](3d)1である. 問題1・5 NiとNi2+の基底状態の電子配置を示せ. 答え Ni:[Ar](3d)8(4s)2, Ni2+:[Ar](3d)8 例題1・6 イオン化工ネルギーの変化を説明する.リンから硫黄へ第一イオン化エネルギーが減少することを説明せよ.解 電子配置はP[Ne](3s)2(3px)1(3py)1(3pz)1 S[Ne](3s)2(3px)2(3py)1(3pz)1である.NとOとの場合と同じく,Sの基底電子配置では3P軌道の一つに2個の電子がある.これらは互いにごく近いので,その反発が強く,その影響が核電荷の増加を上回る. 問題1・6 フッ素と塩素とでは,塩素の第一イオン化エネルギーの方が小さいことを説明せよ. 答え 族の下のほうへいくと原子半径が増加するので、一般に第一イオン化エネルギーは減少する。 例題1・7 電子親和力の変化を説明する.LiからBeに行くところで,核電荷の増加にかかわらず,電子親和力が大きく減少することを説明せよ.解 電子配置はそれぞれ[He](2s)1と[He](2s)2とである.加えた電子はLiでは2s軌道に入る.これに対し,Beでは2p軌道に入らなければならないので,核との結びつきははるかに緩やかである.実際,Beの核電荷はきわめてよく遮へいされているので,電子付加は吸熱的である. 問題1・7 CからNへの電子親和力の減少を説明せよ. 答え もう一個電子を加えるのに、Cでは空のp軌道に入れればよいが、Nではすでに1個電子の入っているp軌道に入れなければならない。 例題2・1 Lewis構造を書くこと.BF4のLewis構造を書け.解 原子が出す価電子の数は3+4×7=31で,1価のアニオンだから,もう1個の電子がある.したがって,計32個の電子を16対として5個の原子の周りに割り振る.解の一つは
問題2・1 PCl3分子のLewis構造を書け. 答え 例題2・2元素の酸化数を求める. つぎの元素の酸化数はいくつか. (a)アジ化物イオンN3-中の窒素 (b)過マンガン酸イオンMnO4-中のマンガン 解 表2・2の規則を順番に適用する. (a)化学種の電荷数は-1,また3個の原子は同一元素だからそれらの酸化数は同じである.したがって3×(Nの酸化数)=-1,すなわち,Nの酸化数=-1/3. (b)酸化数の手和は-1,すなわち(Mnの酸化数)+4×(酸素の酸化数)=-1.酸素の酸化数は-2だから,Mnの酸化数=-1-4×(-2)=+7.つまりMnO4-はマンガン(W)の化合物である. 間題2・2 つぎの元素の酸化数はいくつか. (a)02+十の酸素 (b)PO43-のリン 答え (a)+1/2 (b)+5 例題2・3共鳴構造を書く.NO2F分子の共鳴構造を書き,最も支配的な構造を示せ.解 四つのLewis構造と形式電荷とはつぎのようになる.・
F原子上に正電荷がある構造,また,N原子上に大きな正電荷がある構造は,いずれも低エネルギーであるとは思えない.したがって,N=O結合をもつ二つの構造が共鳴で支配的となるはずである. 問題2・3 NO2-イオンの共鳴構造を書け.
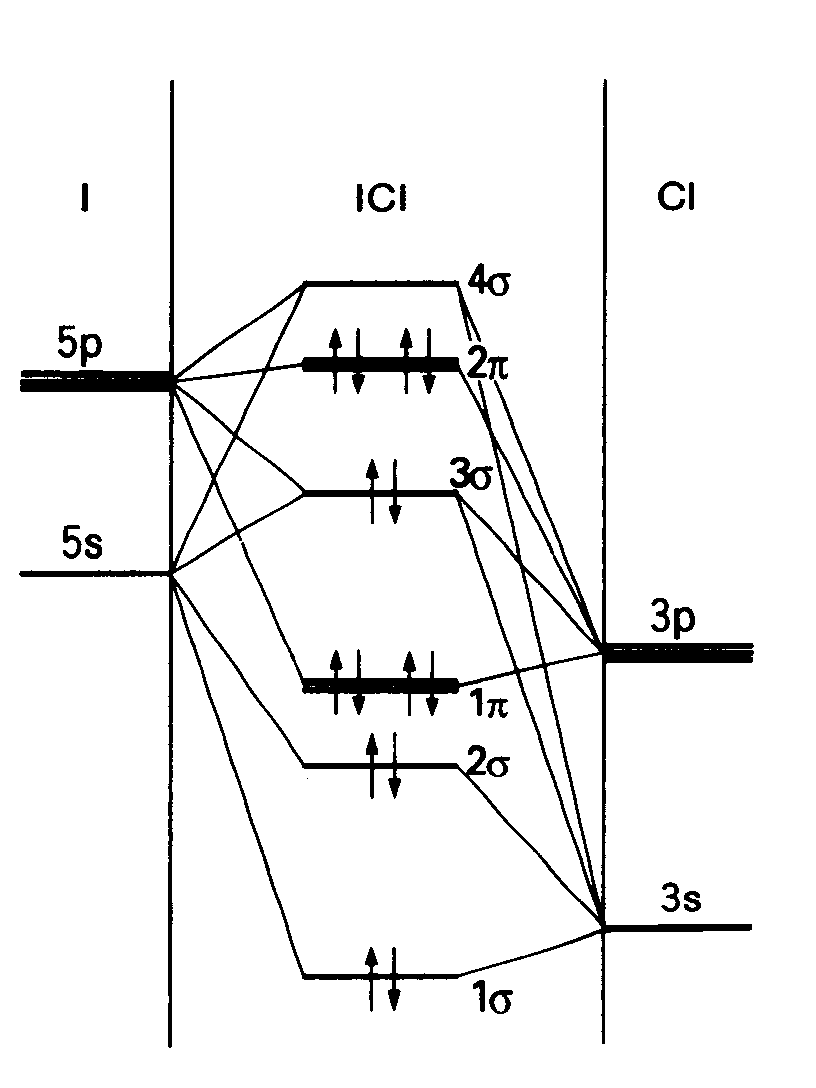
例題2・4 平均結合エンタルピーを用いて標準反応工ンタルピーを推定する.SF4(g)からSF6(g)が生成するときの標準反応エンタルピーを推定せよ.ただし,25℃における平均結合エンタルピーは,F-F結合155,S-F結合(SF4中)343,S-F結合(SF6中)327とする(kJmo1-1単位). 解反応は SF4(g)+F2(g)→SF6(g) 1molのSF6が生じるには,F-F結合が1mo1およびS-F結合(SF4中)が4mo1切れなければならない.これに対応するモルエンタルピーの変化は{155+(4×343)}kJmol-1=+1527kJmol-1.そのときS-F結合(SF6中)が6mol生成するが,それに伴うモルエンタルピーの変化は{6×(-327)}kJmol-1=-1962kJmol-1.したがって全体としてのモルエンタルピー変化は △rH/kJmol-1=+1527-1962=-435 となり,この反応は著しい発熱反応であることがわかる.この反応についての実験値は ΔrH=-434kJmo1-1. 問題2・4 S8(環状分子)とH2とからH2Sが生成するときの標準生成エンタルピーを推走せよ. 答え 24kJmo1-1 例題2・5二原子分子の電子配置を書く.酸素分子02,超酸化物イオン02-および過酸化物イオン022-の基底状態電子配置を書け.解02分子は12個の価電子をもつ.はじめの10個はN2の電子配置と同じであるが,1πuと3σgとの順序が逆転する(図2・10を参照).つぎに電子が入る軌道は二重に縮退した2πg軌道であるから,残り2個の電子は,それぞれ別々にこれらの軌道に入り,スピンは平行になる.したがって,電子配置は02:(1σg)2(2σu)2(3σg)2(1πu)4(2πg)2となる.02の最低エネルギー電子配置は,2個の不対電子が別々のπ軌道に入っているという点で興味深い.それゆえ,02が常磁性(磁場に引き込まれる)なのはこのためである.2πgにはもう2個電子が入れるから 02-:(1σg)2(2σu)2(3σg)2(1πu)4(2πg)3 022-:(1σg)2(2σu)2(3σg)2(1πu)4(2πg)4 となる(ここでは,軌道のエネルギー順が変わらないと仮定したが,おそらくそうではないだろう). 問題2・5 S22-およびCl2-の価電子配置を書け. S22-:(1σg)2(2σu)2(3σg)2(1πu)4(2πg)4 Cl2-:(1σg)2(2σu)2(3σg)2(1πu)4(2πg)4(4σu)1 例題2・6 異核二原子分子の構造を説明する.ハロゲン元素は互いに化合物をつくる.塩化ヨウ素け)IClは,このような“ハロゲン間化合物”の一つである.この基底状態電子配置はどうなっているか.解 まず,分子軌道をつくるのに用いる原子軌道を見つける.C1の原子価殻軌道としては3sと3p,Iの原子価殻軌道としては5sと5Pとがある.第2周期元素の場合と同じようにして,一連のσ軌道とπ軌道とをつくることができ,その準位は図2・17のようになる.結合軌道は主としてClの性質をもち(Clの方が電気陰性度が高いからら),反結合軌道はおもにIの性質をもつ.ここに入れるべき価電子は7+7=14個ある.基底状態の電子配置は結局 (1σg)2(2σu)2(1πu)4(3σg)2(2πg)4 となる.
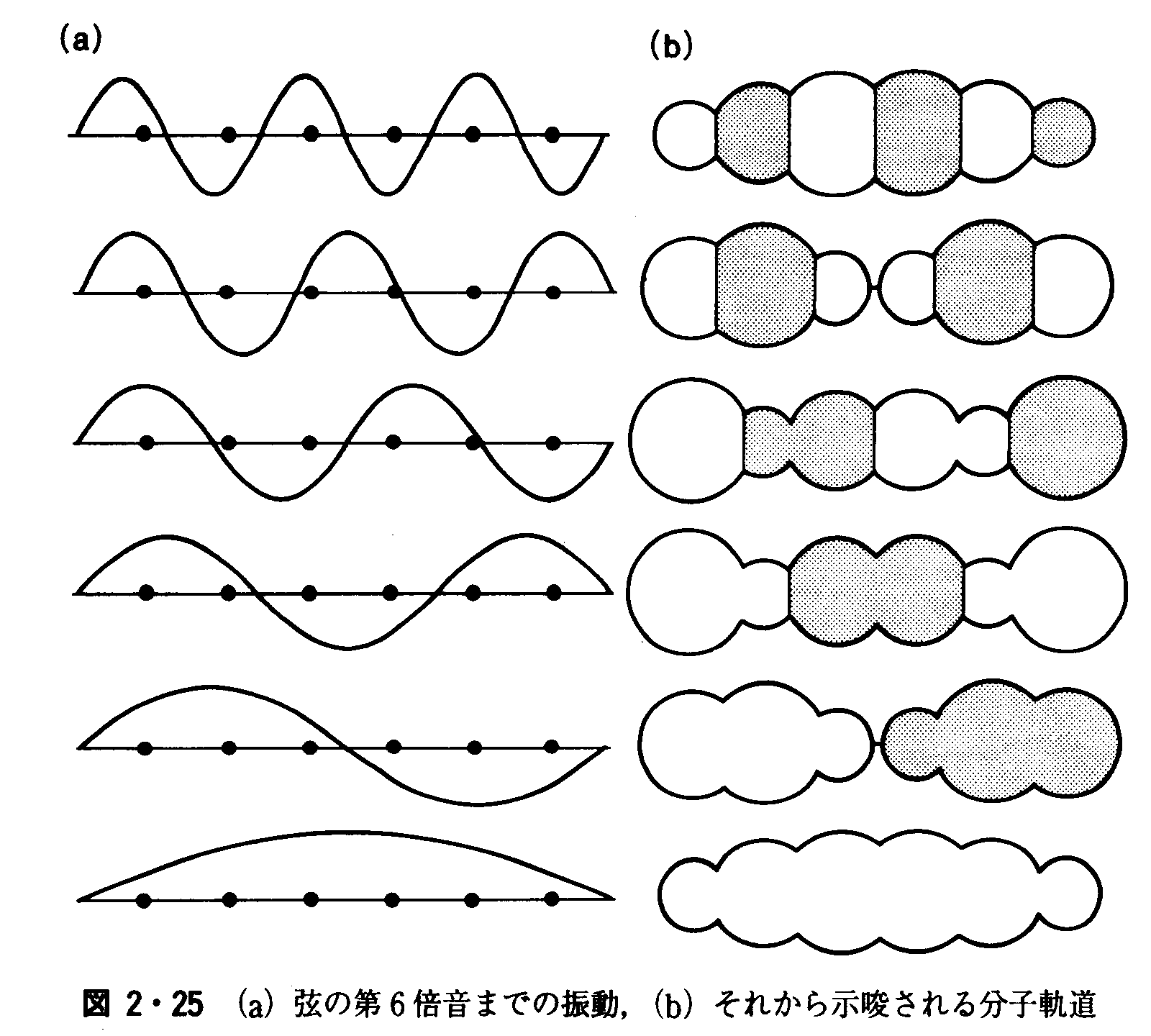
図2・17ハロゲン問化合物IClの分子軌道エネルギー準位の模式図 問題2・6 次亜塩素酸イオンClO-の構造を分子軌道で説明せよ. 答え 図2・17で、左側をCl3sおよびCl3p、右側をO2sおよびO2pで置き換えたような形になる。 例題2・7多原子分子の分子軌道を組み立てる.直線形六原子分子の分子軌道を形成するs軌道の線形結合を描け.解簡単なやり方は,分子軌道と振動する弦の波動との類似性に着目することであl.まず,基音から第6倍音までを表す正弦波を描き〔図2・25(a)〕,つぎに,曲線を原子上の円に置き換える〔図2・25(b)〕.日の大きさは各原子の位置における正弦波振幅と比例するようにし,符号は正弦波の符号に合わせる.
問題2・7環状E8分子のσ分子軌道を組立てよ.後でわかるように,π分子軌道も同じように扱うことができる.このときは,図の円は分子軌道に寄与するp軌道を真上から見たところだと考えればよい.本問題は,ウラノセンの構造と関係がある. 答え 最低エネルギー軌道は完全に対称(節面なし).つぎに二重縮退軌道(⊥節面をもつ分子軌道対)、二重縮退軌道(それぞれ2枚の節面をもつ)、二重縮退軌道(それぞれ3枚の節面をもつ)、最高エネルギー軌道(それぞれの核間に節面がある)の順になる. 例題2・8 電気伝導率の温度依存性からバンドギャツプを決める.ゲルマニウム試料のコンダクタンスGが温度とともにつぎのように変化した.Egの値を推定せよ.T/K 312 354 420G/S 0.0847 0.429 2.86解 σの式からわかるように,化学反応の活性化エネルギーを求めるときと同様にすればよい.一つの試料については,コンダクタンスGは伝導率σに比例するから
対数をとって
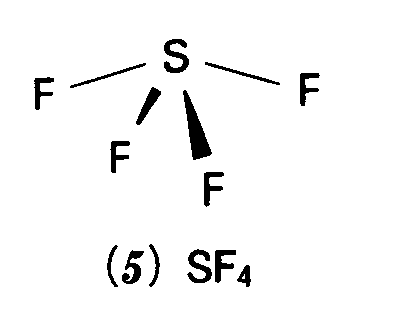
そこで,ln(G/S)を1/Tに対してプロットすれば直線が得られ,その傾斜は-Eg/2kとなる.上のデータからは,この傾斜が-4.26×103Kとなる.k=8.614×10-5eVK-1であるから,Eg=2Ea=0.73eV. 問題2・8 この試料の370Kにおけるコンダクタンスはいくらか.答え 0.723S 例題3・1 VSEPRモデルで分子形を予想する.SF4分子の形を予想せよ.解 まずSF4のLewis構造を描く.
この構造は,中心原子の周りに5個の電子対をもち,それらは三方両錐形の配置をとる(表3・2).1個の孤立電子対の反発が最小になるのは,アキシアル位-ここだとエクアトリアル位の3個の結合電子対と強く相互作用する-ではなく,エクアトリァル位-ここだとアキシアル位の2個の結合電子対と強く相互作用するであるから,孤立電子対はここに来る.そして,S-F結合はいずれも,この孤立電子対から遠ざかるように曲がってシーソーのような形の分子(5)となる.この場合,アキシアル位の結合がシーソーの“板”で,エクアトリアル位の2本の結合が“支点”になる.
問題3・1 XeF2の形を予想せよ. 直線形 例題3・2 測定法の時間尺度を判定する.ある流動的な分子において,位置交換する二つの原子団があり,それぞれ1650cm-1および1655cm-1に振動吸収バンドを示す.この二つの吸収バンドを見分けることが可能なためには,状態の寿命は最小どれほどでなければならないか.解 寿命が1/(2π△ν)より短ければ区別がつかない.これを波数
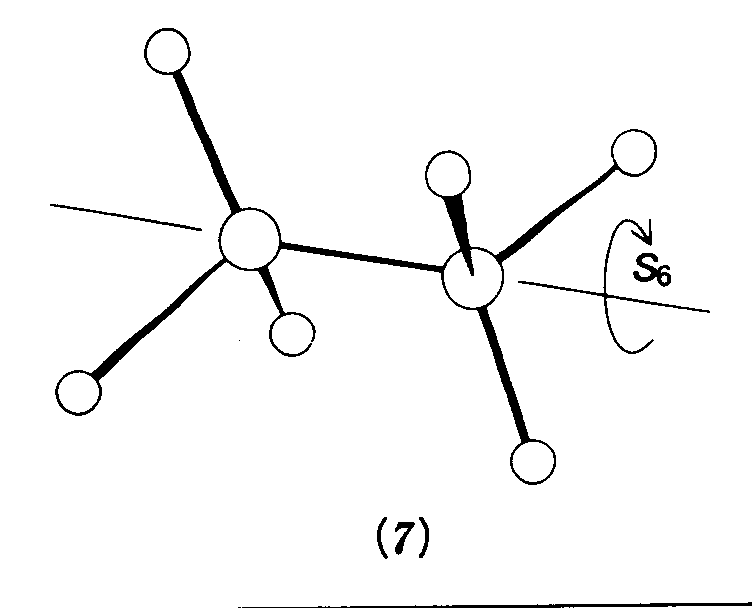
=1×10-12sまたは1ps 1psというと,分子がそれぞれの形をとっている間に約10回振動する時間にすぎない. 問題3・2 ある分子中の二つの原子団のNMRシフトの間隔は550Hzであった.これらの原子団が見分けられるための最小寿命はいくらか. 答え 2.89×10-4s 例題3・3 Walshダイヤグラムを使って分子形を予想する.H2X分子のWalshダイヤグラムを使ってH20分子の形を予想せよ. 解 図3・4の横軸の中間の角度を選んで8個の電子を入れてみると,(1a1)2(2a1)2(1b2)2(1b1)2の配置になる.2a1軌道が占有されていることからみて,直線形分子よりら非線形分子の方が低エネルギーだと期待される, 問題3・3第3周期元素のH2X分子のうち直線形分子が期待されるものがあるか.あるならどれか. 答え 気相中のMgH2 例題3・4対称要素を決める.CH3-CH3分子の形のうちS6軸をもつものはどれか.解 60°回転ざせてから回転軸に垂直な面についての鏡映が元と同じ形であるような形を探す.7がそれであって回映軸はC-Cを通る直線である.これは“ねじれ形”といわれる形で,たまたまエネルギー最低のものでもある.
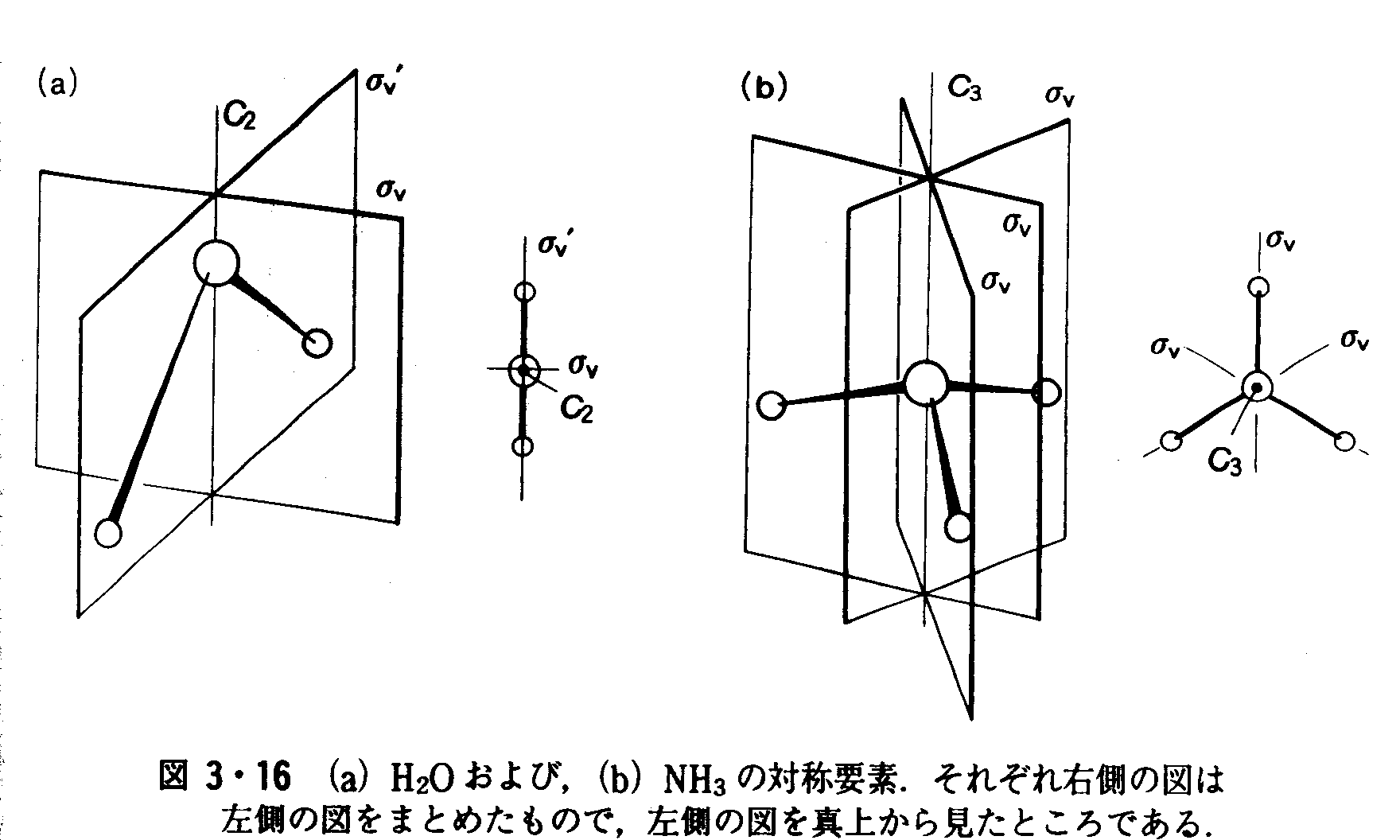
問題3・4 NH4+イオンのC3軸を示せ.このイオンには何本のC3軸があるか. 答え 各NH結合を含むC3軸が4本。 例題3・5 分子の点群を見つける.(a)H20およぴ(b)NH3の属する点群はどれか.解図3・15を使う.それぞれの対称要素を図3・16に示す.(a)H20のもつ対称要素は,恒等(E),1本の2回回転軸(C2),2枚の垂直鏡映面(σvとσv’)である.対称要素の組(E,C2,σv,σv’)は点群C2vに対応する. (b)NH3のもつ対称要素は,恒等(E),1本の3回回転軸(C3),3枚の垂直鏡映面(3σv)である.対称要素の組(E,C3,3σv)に対応する点群はC3vである.
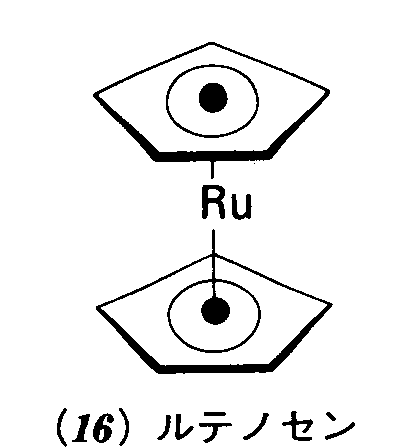
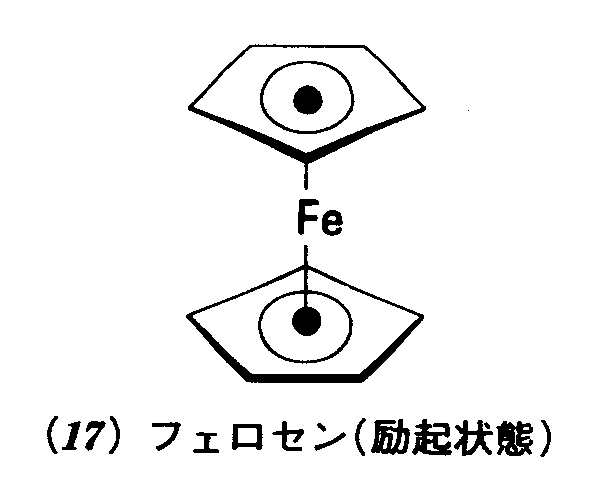
問題3・5(a)平面三角形分子BF3および(b)四面体形イオンSO42-の点群を決定せよ. (a)D3h(b)Td 例題3・6 分子が極性でありうるか否かを判断する.ルテノセン分子(16)は,二つのC5H5環でルテニウム原子をはさんだ五角柱形の分子である.これは極性だろうか. 解 点群がD群または立方群かどうかを決めればよい.もしどちらかであれば永久電気双極子をもつことはありえない.図3・15のチャートによると五角柱はD5h点群に属する.したがって,この分子は無極性でなければならない. 問題3・6 最低エネルギー状態より4kJmol-1だけ上にあるフェロセン分子の形;ねじれ五角柱形である(17).この形のフェロセン分子は極性だろうか.
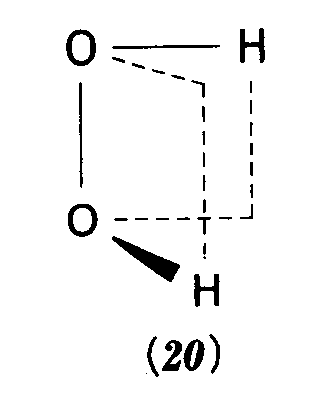
答え 否 例題3・7 分子がキラルか否かを判断する.錯イオン[Cr(ox)3]3-(oxはシュウ酸イオン[02CCO2]2-を示す)は19の構造をもつ.これはキラルだろうか. 解 まず点群を決めるところから始める.図3・15のチャートから,このイオンがD3に属することがわかる.この点群の対称要素は(E,C3,3C2)であって,回映軸(表面に出ているものであれ,隠れたものであれ)を含まない.だから,この錯イオンはキラルであり,したがって,この形の寿命が十分長ければ,光学活性である. 問題3・7 H202のスキュー形(20)はキラルだろうか
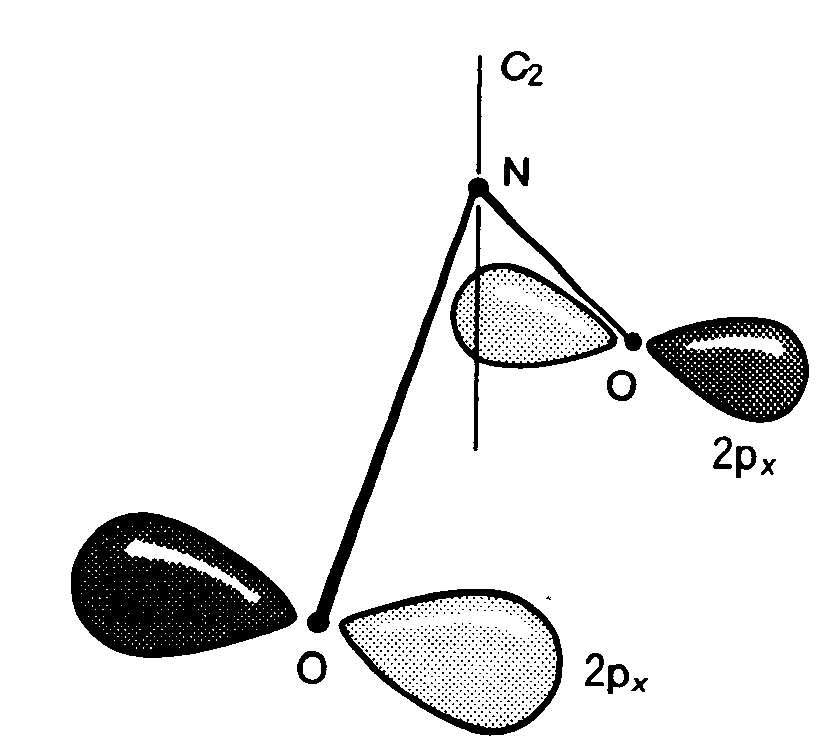
答え キラルである。 例題3・8 指標表を用いて縮退度を判定する. BF3のような平面三角形分子には三重縮退軌道が存在するか. 解 平面三角形分子は点群D3hに属する.この群の指標表(付録3)のE列を見ると縮退度は最大2で,2を超える指標はない.したがって,三重に縮退した軌道は存在しない. 問題3・8 SF6分子は八面体形である.軌道の縮退度は最大いくつか. 答え 三重縮退 例題3・9 軌道の対称型を決める.C2v分子であるNO2の軌道 解 上の線形結合は,図3・24のようになる.C2回転するとΨはもとのままの形になるから,指標は+1,σv’鏡映では,両方の原子軌道は符号が変わるから,Ψ→-Ψとなる.すなわち,指標は-1である.σvでもΨの符号が変わるから,この指標も-1.したがって,指標は E C2 σv σv’ 1 1 -1 -1 となる.これはA2の指標に一致する.したがって,Ψはa2軌道に寄与する.
図3・24 0原子の2px軌道の組 問題3・9 H原子が正方形に並んだ分子の線形結合φ1s(A)-φ1s(B)+φ1s(C)-φ1s(D)の対称型を決定せよ。 答え B2g 例題3・10 対称適合線形桔合を決める.H20(点群C2v)の二つのH1s軌道は,2個の対称適合線形結合φ+=φ(1)+φ(2)とφ-=φ(1)-φ(2)(21)とをつくる.φ+およびφ-の指標を示せ.これらは,Oのどの原子軌道と重なり合って分子軌道をつくるか. 解 C2操作によって,φ+は符号を変えないが,φ-は符号を変える.したがって,指標はそれぞれ+1および-1,鏡映では,φ+は符号を変えないが,φ-の符号はσvで変わるからσv操作に対するφ-の指標は-1.そこで E C2 σv σv’ φ+ 1 1 1 1 φ- 1 -1 -1 1 この表を付録3の指標表に照合すると,φ+はA1,φ-はB2の対称型であることが決まる(付録4を参照すれば,この結論に直ちに達することもできたわけである).指標の右欄によって,02s軌道およぴ02pz軌道がA1対称,02py軌道がB2対称でることがわかる.したがって,可能な線形結合は,
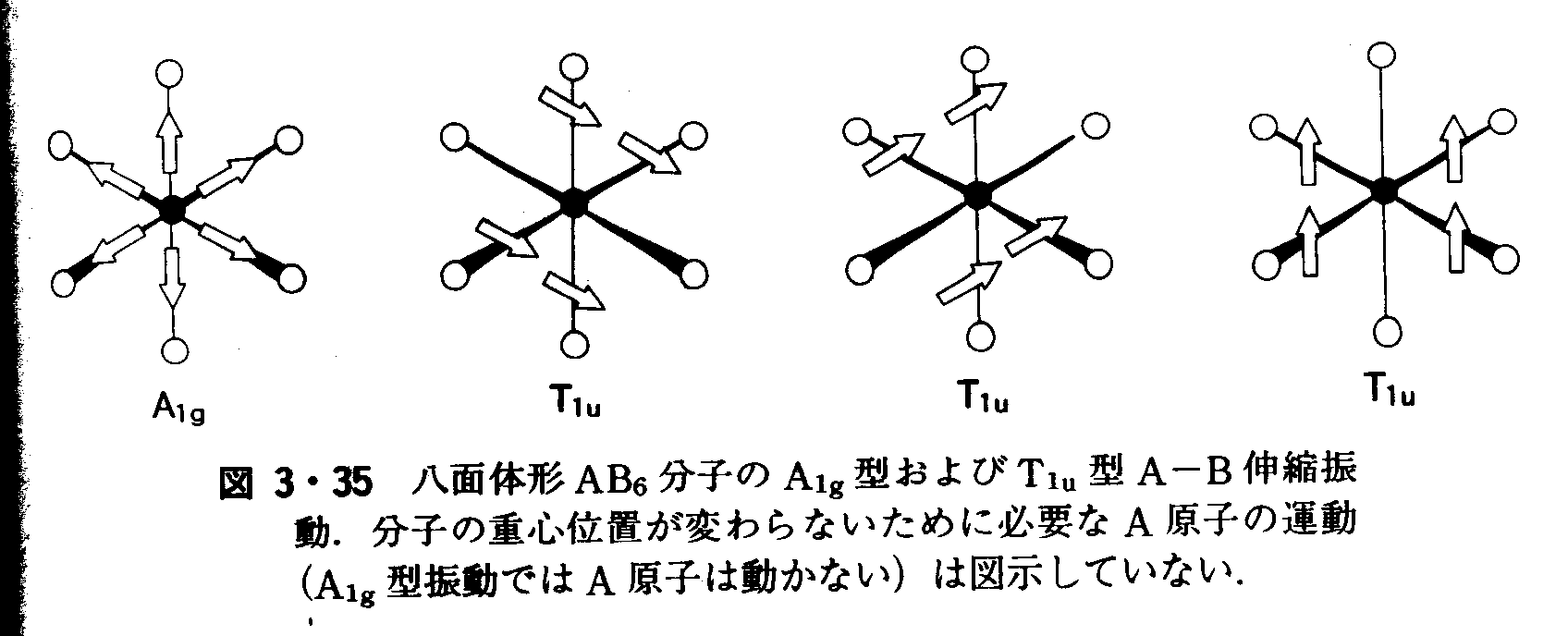
となる.a1軌道は,c1,c2,c3の符号関係次第で結合性あるいは反結合性あるいは中間の性質をもちうる.同様に,c4とc5との符号関係次第で,一方が結合性,他方が反結合性になる. 問題3・10 CH4の4個の水素原子をA,B,C,Dとしたとき,対称適合線形結合φ=φ(A)+φ(B)+φ(C)+φ(D)の対称標識は何か.ただし,φ(J)は水素原子Jの1s軌道である. 答え A1 例題3・11 除外規則を使う.SF6の対称“呼吸”振動はラマン活性である.この振動は赤外スペクトルで検出できるか.解 この分子はOh点群に属し反転中心(S原子)をもつから,除外規則が適用される.すなわち,赤外不活性である. 問題3・11 N20の変角振動は赤外活性である.ラマン活性でもありうるか.答え ありうる。 例題3・12 振動の変位の対称型を決める.図3・32のトランス異性体はD2h対称である.逆対称伸縮振動がB2uの対称型であることを確かめよ. 解D2hの対称操作は,E,C2(z),C2(y),C2(x),i,σ(xy),σ(xz),σ(yz)である.E,C2(y),σ(xy),σ(yz)では,変位ベクトルは変わらない.つまり,指標は+1である.残りの操作ではベクトルの向きが逆になる.したがって指標は-1.結局 E C2(z) C2(y) C2(x) i σ(xy) σ(xz) σ(yz) χ 1 ?1 1 -1 -1 1 -1 1 D2hの指標表と照合すると,対称型はB2uであることがわかる. 問題3・12 トランス異性体の対称伸縮振動がAg対称であることを確かめよ. 例題3・13 八面体形分子の赤外吸収バンドを予測する.SF6のようなAB6分子を考える.A-B振動の線形結合のうち,Oh群のA1g対称型およびT1u対称型のものの略図を描け.解 まず,八面体形の場合に6個のs軌道からつくることのできるSALCが何であるか決める.SALCの軌道がA-B結合の変位に相当し,その符号は変位の位相を表す.付録4のOhのところのA1gとT1uとの図を変位に翻訳すれば,図3・35になる.
答え T1u |
 +
+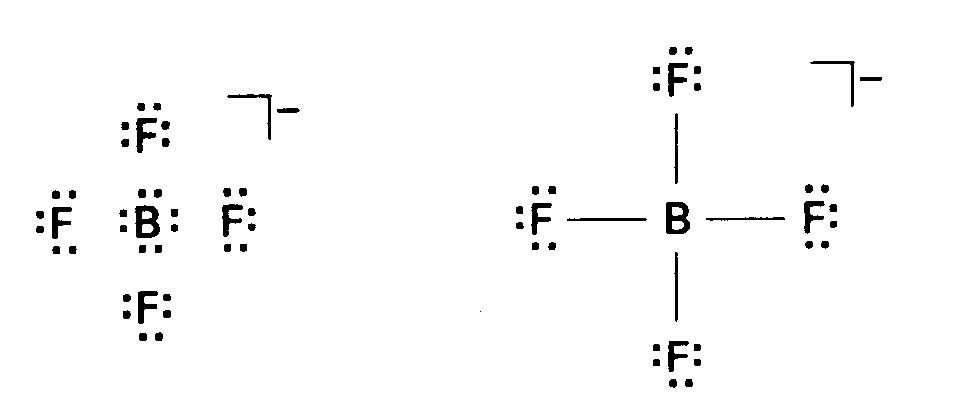 である.負電荷は個々の原子にではなく,イオン全体に割り当てる.
である.負電荷は個々の原子にではなく,イオン全体に割り当てる.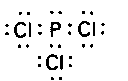
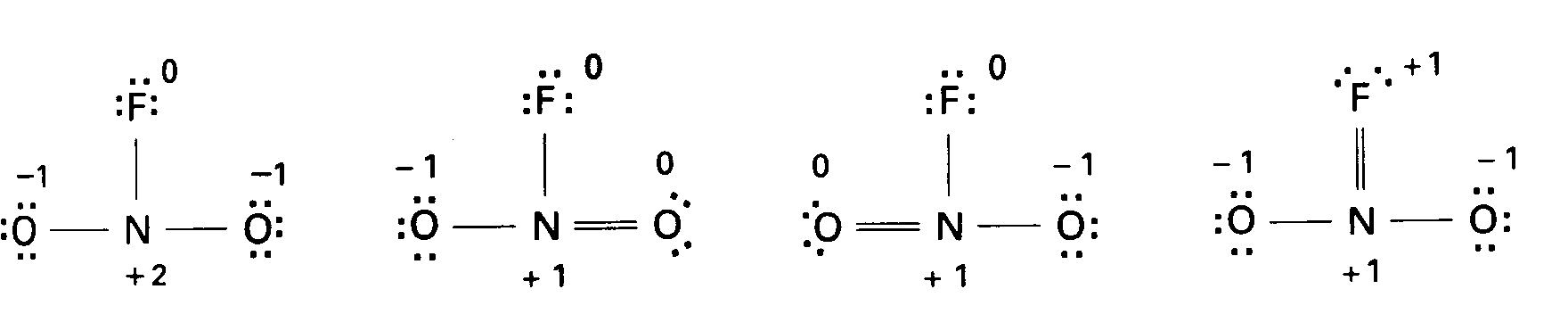
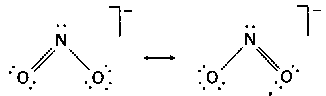
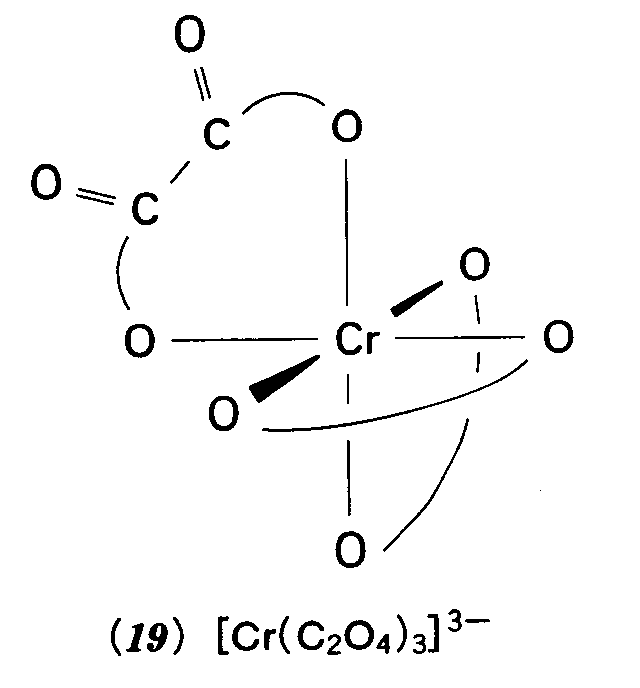
 問題3・13 SF6は1個の赤外吸収バンドを示す.これはA1由来かT1u由来か.
問題3・13 SF6は1個の赤外吸収バンドを示す.これはA1由来かT1u由来か.